摘要:針對OFDM系統頻域中的整數倍頻率偏移、小數倍頻率偏移、采樣鐘頻率偏移和定時偏移等問題,本文提出了相應的
解決方案,并采用
FPGA對各方法進行硬件
電路實現。這些硬件實現方法巧妙,估計精確,能節省大量硬件資源。通過實際的電路時序波形仿真驗證,證明了這些方法的實用性。
關鍵詞:正交頻分復用(OFDM);正數倍頻率偏移;小數倍頻率偏移;采樣鐘頻率偏移;定時偏移
同步部分概述
正交頻分復用(OFDM)系統的一個重要問題是對頻率偏移非常敏感,很小的頻率偏移都會造成系統性能的嚴重下降。另外收發端采樣鐘不匹配,也會導致有用數據信號相位旋轉和幅度衰減,破壞了OFDM子載波間的正交性,降低系統性能。因此在OFDM系統中,頻率偏移和采樣鐘偏移估計的準確度至關重要。
OFDM接收系統的同步部分主要包括以下幾方面:頻率同步、采樣鐘同步和符號定時同步。載波頻率偏移和采樣鐘頻率偏移的存在導致了載波間干擾(ICI)和采樣點增減現象,這就需要頻率同步和采樣鐘同步。同時在解調過程中,接收機是在時域上的任意點開始接收數據的,而OFDM是基于符號的,這就需要檢測到符號的起始位置,否則會因為符號的起始位置的不合理,而導致符號間的干擾(ISI),這就是符號定時同步。
頻域同步估計方法
整數倍頻率偏移估計算法
頻率偏移△f0分成兩部分:整數倍和小數倍子載波間隔頻偏。由于在時域上已經對小數倍頻偏有一個粗略估計和校正,因此頻域內是利用內插導頻信息對整數倍頻偏和剩余小數倍頻偏進行估計校正的。
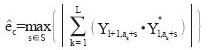 (1)
(1)
式(1)是整數倍頻率偏移估計算法表達式,它是利用連續導頻在發射端為已知固定相位的特性,使用一個長為S的滑動窗作為頻域上一個OFDM符號有效載波起始位置的估計范圍,以窗內的每一個數據作為OFDM符號有效載波的的起始位置,對前后兩個符號在假設的連續導頻位置上的復數據做相關求和,這樣就得到了S個相關值,其中最大值所對應的s即為頻域上一個OFDM符號有效載波起始位置的估計值,也即為整數倍頻偏估計值。
其中L是連續導頻個數;ak是一個符號內第k個連續導頻的序號;Yl,ak是FFT輸出的第l個符號的假設第k個連續導頻位置上的復數值;S是整數倍頻偏的估計范圍,也即為滑動窗長,s是窗口移動值,s∈S; 是S路相關和的最大值,其對應的s即為整數倍頻偏的估計值。
是S路相關和的最大值,其對應的s即為整數倍頻偏的估計值。
小數倍頻率偏移和采樣鐘頻率偏移估計算法
在OFDM系統的接收端,實際的第m個子載波的實際解調頻率為f'm=f'0+mF',這里,f'0為本地解調載波頻率,F)=F'0N,N為子載波個數,F'0為接收機壓控晶振輸出的采樣頻率。由此可以看出,在第m個子載波上,載波頻偏和采樣鐘偏移的聯合效應是大小等于△fm的子載波頻偏,這里△fm=△f0+m•△F0N,△f0=f'0-f0,△F0=F'0-F0,f0和F0分別為發射端的中心載波頻率和采用頻率。當將整偏校掉后,這里的△f0僅為小數倍的子載波間隔。
設pi為導頻點位置,pi∈P,P為導頻點位置集合;i=0,1,…,K-1,K是P的基數;△fpi為第pi個導頻點上相關結果的頻率部分,這個值以下用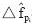 表示為估計結果。定義
表示為估計結果。定義 ,同時考慮到在第pi個子載波上的估計誤差ei,則:
,同時考慮到在第pi個子載波上的估計誤差ei,則:
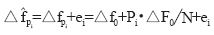 (2)
(2)
其中,△fpi為在第pi個導頻點上的頻率偏移和采樣鐘偏移之和,現令 為所需估計的向量參數,式(2)就可以寫作:
為所需估計的向量參數,式(2)就可以寫作:
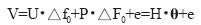 (3)
(3)
其中,

由于估計是基于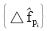 的,因此將向量V稱為觀察向量,方程式(3)稱為觀察方程。線性最小平方估計就是在觀察向量給定的條件下,根據觀察方程估計向量
的,因此將向量V稱為觀察向量,方程式(3)稱為觀察方程。線性最小平方估計就是在觀察向量給定的條件下,根據觀察方程估計向量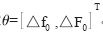 。根據最大似然估計原理,使得向量V的線性函數
。根據最大似然估計原理,使得向量V的線性函數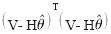 取得最小值時,得出
取得最小值時,得出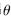 的估計值
的估計值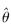 。對式
。對式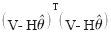 求導并使之為零,可得:
求導并使之為零,可得:
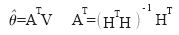 (4)
(4)
公式(3)是在先得出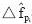 ,i=0,...,K-1的基礎上求得的,而
,i=0,...,K-1的基礎上求得的,而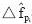 可以通過在導頻位置對前后兩個OFDM符號做相關運算來求。
可以通過在導頻位置對前后兩個OFDM符號做相關運算來求。
頻域符號定時偏移估計算法
時域定時的不準確就要求頻域內進一步對OFDM符號定時進行校正。由于時域內保護間隔是數據信號最后L個采樣點的完全復制,所以由FFT循環移位定理可知:符號定時的偏移所引起的子載波上相位旋轉和子載波序號k成正比。由于導頻信號插入位置已知,且其具有相位已知特性,這使得我們可以利用符號內插導頻載波間相位變化來做細符號定時同步,并與粗符號定時同步結合起來,得到一個準確的符號起始位置。
設 是第j個OFDM符號定時偏移在相鄰導頻點上所引起的相位偏移之差,
是第j個OFDM符號定時偏移在相鄰導頻點上所引起的相位偏移之差, 為第j個OFDM符號所估計出來的細定時。則
為第j個OFDM符號所估計出來的細定時。則 和
和 可表示為:
可表示為:
 (5)
(5)
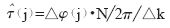 (6)
(6)
其中,L為散布導頻個數;N為一個OFDM符號中有效子載波的個數;Xj,k是第j個符號的第k個散布導頻復值;△k為兩個相鄰的子載波序號的差值。
頻域同步部分的FPGA電路實現模塊
頻域同步電路模塊各單元的工作原理如圖3.1所示。這里使用Altera公司生產的StratixⅡEP2S60的FPGA芯片來實現。

圖3.1 FFT后同步塊方框圖
FFT模塊輸出復數據經過一個OFDM符號的FIFO模塊延遲后,和當前的OFDM復數據進行相關,以實現在整數倍頻偏估計和小數倍頻率偏移算法中所需要的前后兩個符號的對應導頻相關運算,其相關結果為32位的復數據。
整數倍頻率偏移估計模塊
將相關單元輸出的復數據的實虛部符號位送到整數倍頻偏估計單元中進行整數倍頻偏估計。為了節省芯片資源,這里我們將估計整數倍頻偏的算法加以簡化,用相關后的復數據在導頻位置上的實虛部的符號位來估計整數倍頻偏值。下面的仿真的電路波形圖證明這樣實現整偏估計算法是可行的。它的輸入為相關單元輸出的復數據實虛部的符號位和此復數據的載波同步位置,輸出為整數倍頻偏估計值。
小數倍頻率偏移和采樣鐘頻率偏移模塊
首先對相關單元模塊輸出的復數據的實虛部進行歸一化,然后求歸一化單元輸出的16位復數據的相角,同時用RAM的讀地址和讀使能信號分別控制讀取存有矢量A和矢量B數據的ROM表中的數據。其中矢量A和B分別為線性最小平方估計算法中矩陣AT的第一行和第二行矢量,用此相角分別和讀出的矢量A和矢量B在一個符號內進行相乘累加,再根據保護間隔的不同,乘以相應的系數,便可分別得到小數倍頻偏和采樣鐘頻率偏移的估計值。
細定時估計模塊
考慮到定時估計范圍的問題,該模塊利用四個符號的散布導頻進行定時估計。將當前符號的散布導頻值及從RAM中讀出的前三個符號的散布導頻值按一定順序排列,并做相鄰導頻相關。將相關后的復數據的實虛部分別取絕對值累加,并將二者的累加和進行歸一化處理后進行查表,從而得出復數的相位值。這個相位即為符號定時偏移所引起的旋轉相位。再對此相位做如公式(6)的運算,這樣就得到了符號定時偏移的整數和小數部分的和,然后將其送到求整函數中,從而得到符號定時偏移的整數部分。將這個值經過并/串變換后送到前端時域同步部分,去調整FFT窗位。
電路仿真
其仿真條件為:瑞利信道,SNR為15dB,載波頻偏設為-14.9倍子載波間隔(即整數倍頻偏值為-15,小數倍頻偏值為0.1倍子載波間隔),采樣鐘偏移為50ppm,保護間隔長為512,定時符號偏移為-100個采樣點。此電路工作頻率為10MHz。輸入的16位復數據由MATLAB仿真程序產生的。
整數倍頻率偏移電路仿真
由于電路波形中無法表示小數,因此將各小數進行“擴展”,其表示皆為二進制數據,以下同。在圖4.1中,out_re[31]和out_im[31]分別是前后兩個OFDM符號中對應子載波相關結果的實虛部的符號位,int_freqoffset[5..0]和syn_int分別是整數倍頻偏估值和其有效起始位置脈沖。

圖4.1 整數倍頻偏估計部分的電路仿真波形圖
由于整數倍頻偏在每一符號的結束處才能估計出來,所以syn_int在每一個符號的結束處出現,其后即為當前符號的整數倍頻偏值。由于本算法利用了4個符號的連續導頻,故圖4.1中,從第四個syn_int后的int_freqoffset[5..0]才是當前符號的整數倍頻偏估計值。由仿真波形可看出,估出的整數倍頻偏與仿真數據中所假設的一致。故用此算法的簡化形式可以準確地估計出整數倍頻偏值。
小數倍頻率偏移及采樣鐘頻率偏移估計的電路仿真
sernum[1..0]表示前級輸入的符號類型;syn為輸入復數據中的有用數據起始脈沖;rein[15..0]和imin[15..0]分別為FIFO模塊輸出復數據的實虛部;syn_offset為小數倍頻偏和采樣鐘偏移估計結果的起始位置;fri[14..0]和qdelt[14..0]為小數倍頻偏估計值和采樣鐘偏移估計值,它們由1位符號位和14位小數位組成。這里的小數位數是根據其估計范圍和估計精度要求來確定的。
在圖4.2中,小數倍頻率偏移和采樣鐘頻率偏移估計模塊使用連續導頻進行估計。在每個符號末,syn_offset高電平有效時,fri[14..0]和qdelt[14..0]才是當前符號的小數倍頻率偏移和采樣鐘頻率偏移估計值。波形中的估值與實際數據的對應關系如表4.1所示。

圖4.2 小數倍頻偏和采樣鐘偏移估計單元的電路仿真波形圖


 加好友
加好友  發短信
發短信

 Post By:2010-11-12 15:27:45
Post By:2010-11-12 15:27:45


 加好友
加好友  發短信
發短信

 Post By:2010-12-2 14:54:25
Post By:2010-12-2 14:54:25
